This page shows how a space elevator could exist off the equatorial plane. It shows a string in equilibrium between 3 forces: gravitation, centrifugal force and tension from the anchor point on the ground. Since creating this page I have written a paper on the subject that has a lot more detail. You can find the paper here, or my slides from the third annual space elevator conference here.

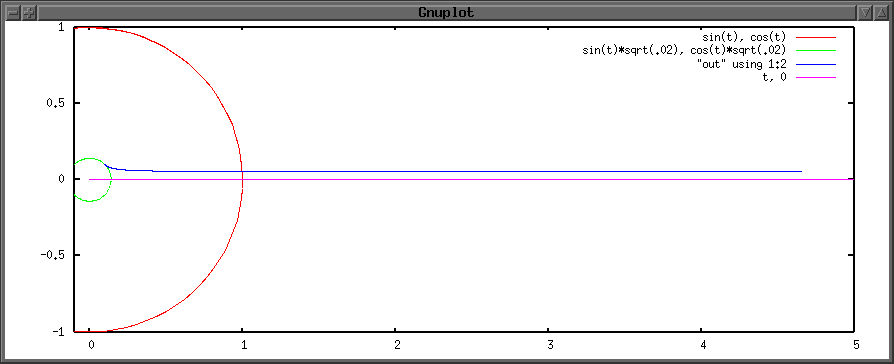
In this figure, the green circle is the Earth, the red circle shows geosynchronous altitude, the pink line is the equatorial plane, and the blue curve is the space elevator. Please ignore the numbers on the graph, I did not bother with the actual physical constants; however, the general shape of the elevator is correct. Moreover, the string that I used here is uniform, it does not get thicker when the tension increases. That would also change the shape of a real elevator slightly. Just like an equatorial elevator, this elevator could be shortened by using a counter-weight. In that case, the shape of the elevator would change slightly, though.

As you can see, the elevator is entirely above the equatorial plane. The y-axis component of gravitation tries to pull the whole elevator towards the equator. The force excerted by the anchor point is the only thing preventing the elevator from "falling" towards the equatorial plane.

The configuration that is shown is static. The elevator doesn't swing around above and below the equatorial plane. Note that the center of gravity of the elevator is not in geosynchronous orbit. There are two reasons why this is not a problem. First, the earth is exerting a force on the elevator, so the elevator is not an isolated object in orbit. Second, but less important in this instance, the elevator is not infinitesimal compared to the gravity field in which it is orbiting. Therefore, it shouldn't be expected to exactly follow the simple orbital rules that apply to point objects.

In my opinion, the main drawback with the off-center elevator is that there is a huge tension on the anchor point. This means that the cable will have to be heavier. Also, it means that a way has to be found to get the anchor setup. When building an equatorial elevator, there is no need for a force from the anchor point, so the elevator can simply be extended up and down until it reaches the ground. The off-equator elevator needs a force from the ground to stay off equator, so that strategy won't work. The only idea I can think of is to make an equatorial elevator, and then move the anchor point to the desired position. I am not sure how hard pulling the elevator into place would be, because I did not do the simulation with real numbers.

If you put a higher tension on the elevator from the anchor point, other neat configurations are possible. For example, with just the right tension from the anchor, a single strand can join two points that are at opposite lattitudes.

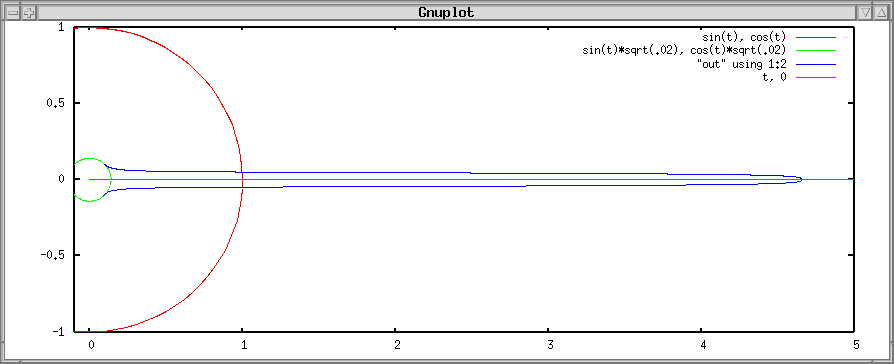
If the tension increases even further, the elevator crosses the equatorial plane at a lower altitude, and then does some really strange things. Such an elevator would have to be infinitely long to remain in place, so it is just a concept.

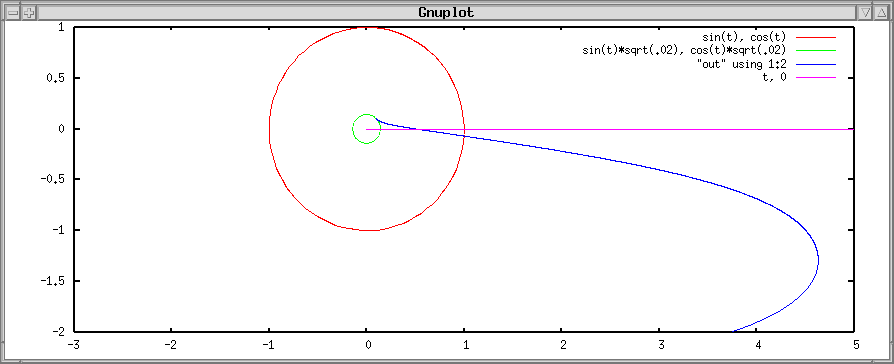
By cutting the elevator off at the equator and joining it with another branch that comes from the opposite latitude, and connecting that to an equatorial elevator, you get the forked elevators that are described in science fiction (for example in Kim Stanely Robinson's Mars trilogy). But since the tension at the ground is even greater than it would have been with the simple off-equator elevator, I don't really get the point.