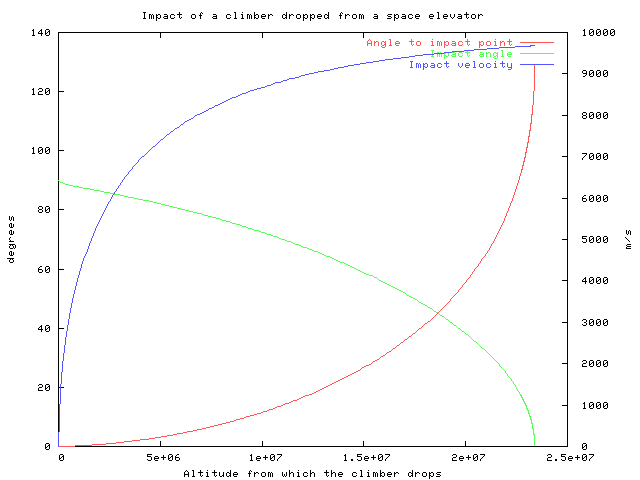
This graph shows how a climber that lets go of the space elevator will impact the earth. The values that are plotted are:

In red, the difference in longitude between the elevator and the impact point. The impact will be to the East of the elevator.
In green, the angle at which the climber will impact the Earth. For low altitudes the climber crashes nearly vertically. At the dropping altitude increases, the impact becomes nearly horizontal.
In blue, the velocity at which the climber impacts the Earth. Atmospheric effects are not considered, so this is about the velocity at which the climber enters the atmosphere.

Impact data of a climber falling from a
space elevator

This data was generated using a simple C program and plotted with this gnuplot script. This program simply simulates the fall of the climber from various altitudes under the effect of gravitation. Aerodynamic effects are not taken into account. David Forslund has kindly translated the code into Java.

1. Minimum orbital altitude

The upper limit of this graph corresponds to the climber successfully entering Earth orbit (in fact because of atmospheric effects, the limit should be a bit higher). We can easily calculate the minimum orbital altitude using conservation of momentum and energy. It is about 23.4 thousand kilometers. Using Kepler's third law, we can check the maximum difference in attitude between elevator and the impact point. The theoretical result is 129.5 degrees. The details of the calculations can be found in this Maple sheet.

2. Consequences on elevator positioning

It is impossible to position the elevator so that it is 129.5 degrees from the nearest land. However, the distance between the cable and the impact point exceeds 45 degrees over less than a 5000 km range of altitudes. If the nearest land is at least 45 degrees away from the cable, that would severely reduce the chances that a climber will fall on land. If a 90 degree safe zone was used then the range of altitudes is reduced to 700 km, that a climber would cross in under 4 hours.

3. Effect of initial vertical velocity

In the event of a cable break, climbers might fall with an non-zero initial vertical velocity. In that case, the impact point will be different from what is computed here. Determining what a reasonable initial velocity would be is a complex problem as it involves many assumptions on how the cable behaves when it breaks. This problem is left as future work.